냉각탑에 관련된 열역학 기초사항

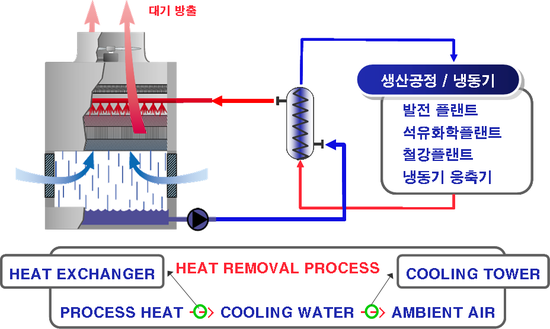
출 처 : http://blog.naver.com/criok707

“냉각탑 이란?”에서 언급한 기계장치에서 발생된 폐열을 최종적으로 대기로 방출시키는 냉각탑에 대해 기술적으로 설명을 하기 위해서는 열 역학과 관련한 몇가지 내용을 알아 둘 필요가 있어 다음과 같이 요약해 본다.

열역학적 온도 (Thermodynamic Temperature)
- 일반적으로 온도를 측정하는 온도계는 열에 의한 물질의 팽창, 전기저항 및 열기전력의 변화 등을 이용한다. 그런데 온도계에 사용하는 물질에 따라 이들 성질이 달라짐으로 온도계의 종류에 따라 서로 다른 온도를 표시하게 된다. 이와 같은 불편을 없애기 위해서는 온도계에 사용하는 물질의 종류와는 무관한 온도 눈금을 정의할 필요가 있다. 이런 목적으로 정해진 온도가 열역학적 온도인 것이다.
- 카르노 사이클 (Carnot Cycle) 에서 고온열원이 작동유체에 준 열량 Q₁과 작동유체가 저온열원에 준 열량 Q₂와의 비율인 열효율은 작동유체에 관계 없이 두 열원의 온도만으로 정해진다. 지금 임의의 한 고온열원의 온도 T₁을 기준으로 하여 미지의 저온열원의 온도 T₂를 구하는 관계식은 다음과 같다.
  - T₂ = (Q₂ / Q₁) * T₁
- 이 관계식에서 기준온도인 T₁의 수치에 따라 열역학적 온도가 여러가지로 변하므로 물의 3중점 (물, 얼음, 수증기가 동시에 존재하는 평형온도) 의 온도인 273.16 K을 기준으로 한 것을 온도눈금의 단위로 한 것을 열역학적 온도라 하며 Kelvin의 절대온도라 부르며 K로 표기한다.
- 물의 3중점온도는 정확히 0.01℃임으로 열역학적 온도눈금의 영점은 순수한 물의 3중점보다 0.01℃ 낮은 온도인 273.15가 된다. 따라서 절대온도와 섭씨온도와의 관계는 T (K)= t (℃)+ 273.15가 된다.
열량의 단위
- SI (SI = The International System of Units) 단위에서 열량의 단위는 일의 단위와 동일한 주울 (Joule)을 사용한다.
- 1 J = 1 N x 1 m = 1 N∙m (참고: 1 주울은 1뉴톤의 힘으로 힘과 같은 방향으로 1미터를 옮기는데 필요한 일)
- 1 N = 1 ㎏ x 1 m/s² = 1 ㎏∙m/s²(참고: 1 뉴턴은 질량 1 ㎏의 물체에 1 m/s²의 가속도를 일으키게 하는 힘을 말한다. SI단위에서 무게는 질량 ㎏을 사용함.)
  - 주석 1 : 1 ㎏f = 1 ㎏ x 9.80665 m/s² = 9.80665 ㎏∙m/s² = 9.80665 N
  - 주석 2 : 1 ㎏f-m = 9.80665 N-m = 9.80665 J
  - 주석 3 : 공학단위계에서 사용하는 ㎈와 J간의 관계는 계량법에 따르면 1 ㎈ = 4.186047 J ≒ 4.186 J (4.186047 = 3600 / 860에서 얻어진 것임.)
  - 주석 4 : 공학단위계에서 사용하는 ㎉와 ㎏f-m간의 관계는 1 ㎉ = 4186.047 J = 4186.047 / 9.80665 ㎏f-m = 426.858 ㎏f-m ≒ 427 ㎏f-m (1 J은 1 뉴톤의 힘으로 1 미터를 옮기는 필요한 일이라면, 1 ㎉는 427 ㎏f를 1 미터 옮기는데 필요한 일이 되는 셈이다.)
  - 주석 5 : 열량의 US단위는 BTU이며 1 BTU = 0.2520 ㎉ = 0.2520 x 4186.047 J = 1054.884 J ≒ 1055 J
일률 (동력)의 단위
- 1 Joule이란 1Ω (ohm)의 저항에 1A(Ampere)의 전류가 흐를 때의 1 초간의 발열량으로 정의함으로 Joule 대신에 Watt-second (Ws)를 사용하면 1 J = 1 Ws가 된다. 따라서 1 W = 1 J/s 성립된다.
- 1 W = 1 J/s
- 1 kW = 1000 J/s = 1000 * 3600 J/h = 1000 * 3600 / 4.186047 ㎈/h = 860000 ㎈/h = 860 ㎉/h (1kW는 1시간 동안 860 ㎉의 발열량 (일))
- 1 kW = 1000 J/s = 1000 N∙m/s = 1000 kg∙m/s² ∙m/s = 1000 / 9.80665 kgf∙m/s²∙m/s / (m/s²) = 101.9716 ㎏f m/s ≒ 102 ㎏f m/s (1kW는 1초간에 102 ㎏f를 1 미터 옮기는 일률)
- 1 kW = 860 ㎉/h = 860 ㎉/(3600 s) = 101.9716 ㎏f m/s 로 부터 1 ㎉ = 101.9716 * 3600 s / 860 ㎏f m/s = 426.85786 ㎏f m ≒ 427 ㎏f m
- (참고 : 열 에너지는 다른 에너지로 또는 에너지는 열로 변환된다. 이것이 열역학의 기본법칙인 제1법칙이며 흔히 에너지보존법칙이라 한다. 전문적인 정의는 “열은 본질상 일과 마찬가지로 에너지의 일종이며, 열을 일로 또 일을 열로 변환시킬 수 있다”이다. 열량 Q ㎉가 일 W㎏f∙m로 변환될 때 열역확의 제1법칙에 따른 관계식은 Q = AW ㎉로 표기되며 여기서 A를 일의 열당량 (Thermal Equivalent of Work) 이라고 하며 A = 1 / 427 ㎉/(㎏f∙m)가 된다.
비열의 단위
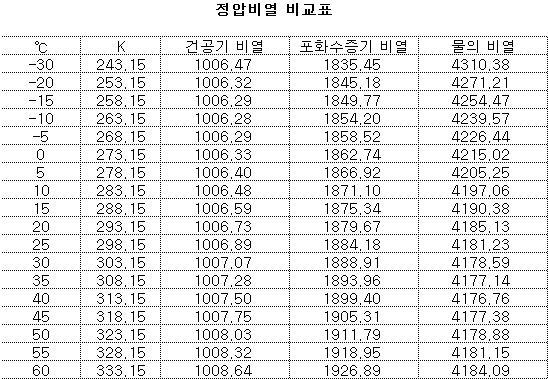
- 단위 질량의 물체의 온도를 1K 올리는데 필요한 열량 (J)을 비열이라고 하며 SI 단위에서는 J/(㎏∙K)를 사용한다. 비열은 온도변화에 거의 비슷한 값이지만 상태변화에 따라서는 값이 현저히 달라진다. 특히 포화수증기 및 물의 경우는 더욱 심하다. 아래 도표는 건공기, 포화수증기 (주어진 온도에서 공기가 포화상태일 때의 수증기만을 의미) 및 물의 정압비열을 나타낸 것이다. 단위는 J/(㎏∙K) 이다.
- SI단위에서 사용하는 J/(㎏∙K)와 공학단위계에서 사용하는 ㎉/(㎏∙℃)와 간의 관계는 다음과 같다.
  - 1 J/(㎏∙K) = 1/4.186047 ㎈/(㎏∙K) = 1/4186.047 * 1000 ㎈/(㎏∙K) = 1/4186.047 ㎉/(㎏∙K)
- 상태변화란 계 내의 작동유체가 한 상태에서 다른 상태로 변화하는 것을 말하며 어떤 방법으로든지 원래의 상태로 되돌릴 수 있다면 이 변화를 가역변화 (Reversible Change) 라 하며, 여하한 방법으로도 모든 것을 되돌아 가게 할 수 없을 때의 변화를 비 가역변화(Irreversible Change) 라 한다.
- 가역변화는 열전도나 마찰에 의한 열의 발생 등이 수반되지 않는 것임으로 자연계에서는 엄밀하게 볼 때 현실성이 없음으로 자연계에서는 비 가역변화가 일어난다고 볼 수 있다. 상태변화의 변화과정에서 체적의 변화가 없는 경우의 비열을 정적비열 (cv) 이라고 하며, 압력의 변화가 없는 경우의 비열을 정압비열 (cp) 이라고 한다. 일반적으로 같은 온도에서 정압비열이 정적비열에 비하여 값이 약간 높다.
- 비열은 동일한 상태변화에서도 온도가 변화면 다른 값을 갖게 되며 비열은 온도만의 함수이다. 한편, 온도 T₁K에서 T₂K로 상승시키는데 필요한 열량을 계산하기 위해서는 유체의 무게에 평균정압비열 (Cpm)을 사용하게 되는데 이때의 평균비열은 온도 (T₁ + T₂) / 2 한 평균온도에서의 비열이다. 참고로, 밀폐식 냉각탑의 열량해석에서는 정압비열만을 사용하며 온도변화가 있는 경우는 평균정압비열을 사용함을 기억하기 바란다.
잠열과 감열 (Latent Heat & Sensible Heat)
- 액체를 가열하면 열 에너지는 먼저 액체의 온도상승과 체적팽창에 사용되며 (액체의 경우 체적증가가 보통의 경우 매우 작다.) 다시 가열을 계속하면 어떤 온도에서 증발이 일어난다. 일정 압력하에서 증발이 일어나기 시작하면 온도 상승은 중지된다.
- 이 때 가해진 열 에너지는 내부 에너지의 증가와 체적팽창에 필요한 일을 하게 된다. 일정한 압력하에서 액체 1㎏을 전부 증발시키는데 필요한 열량을 증발열 또는 증발의 잠열이라고 한다. 한편, 감열은 단위 질량의 물체의 온도를 상승시키는데 필요한 열량을 의미한다.
- 증발잠열 @ 273.15K (0℃)= 2.5016 x 10^6 J/㎏
  - 주석 1 : 공학단위계에서 사용하는 ㎉/㎏으로 환산하면 다음과 같다. 증발잠열 = 2.5016 x 10^6 J/㎏ = 2.5016*10^6/4186.047 ㎉/㎏= 597.6 ㎉/㎏
  - 주석 2 : 자연상태의 물이 증발될 때의 증발잠열은 물의 온도에 따라 다르다. 물의 온도가 높을 수록 증발잠열은 줄어든다. 위의 증발잠열은 물의 온도를 0℃를 기준으로 한 것이며, 물의 온도가 30℃인 경우는 2.4307 x 10^6 J/㎏, 50℃인 경우는 2.3829 x 10^6 J/㎏이다.
압력의 단위
- 압력 (Pressure)은 유체에 의한 단위면적당의 수직력이다. 단위로는 Pa, N/㎡, Bar, kg/㎡ 등을 사용한다. 압력계 등의 실용상의 단위로는 ㎏/㎠ (at로 표기) 흔히 사용하며 이것을 공업기압이라고 한다.
- 1 표준기압: 0℃에서 수은주가 760 mm (0℃에서의 수은의 밀도 = 13.5951 g/㎤)가 되는 압력이며 이것을 1 atm (Atmosphere의 약어)으로 표시한다.
- 1 atm = 760 mmHg = 760 * 13.5951 mm g/㎤ = 760 * 13.5951 * 1/10 ㎝ * 1/1000 ㎏f /㎤ = 1.0332276 ㎏f/㎠ =1.0332276 ㎏f/(1/100)³ ㎥ = 10332.276 ㎏f/㎡ = 10332.276 * 9.80665 ㎏∙m/(s²∙㎡) = 101325.0114 N/㎡ ≒ 101325 N/㎡ = 101325 Pa
- 위의 관계식은 대기의 온도가 0℃일 때 성립되는 표준기압이며 고도, 시간 및 장소에 따라 변화는 대기압과는 구분이 되어야 한다. 온도가 상승하면 수은은 팽창함으로 동일 압력에 대해서 수운주의 높이는 약간 올라가게 된다. 따라서 열해석에서는 절대압력 (Absolute Pressure, ata로 표기)을 사용하며 온도보정을 통해 측정한 기압을 보정하면 절대압력을 얻게 된다.
  - 가령 대기의 온도가 25℃ 일 때 측정한 수은주 기압계가 740 mmHg를 지시하였다면 절대압력은 얼마인가? 절대압력 = 740 * (1 – 0.000172 * 20℃) = 737.454 mmHg가 된다.
비체적 (Specific Volume)
- 단위중량의 물질이 차지하는 체적을 비체적이라고 하며 v ㎥/㎏f로 표시한다. 단위체적의 물체의 중량을 비중량 (Specific Weight)이라고 하며 γ㎏f/㎥로 표기한다. 따라서 비중량의 역수는 비체적인 관계가 성립한다. 즉, v = 1 / γ 또는 vγ=1
- 밀도 (Density) ρ는 단위체적에 대한 물체의 질량이며 비중량 γ와의 관계는 ρg = γ ㎏f/㎥이다. (여기서 g는 중력가속도이며 g = 9.80665 m/s² 이다.)
- ρ = γ ㎏f/㎥ / (9.80665 m/s²) = γ ㎏/㎥ * (9.80665 m/s²) / (9.80665 m/s²) = γ ㎏/㎥
- 비중 (Specific Weight) δ는 동일체적의 물의 질량에 대해서 몇 배인가를 표시하는 무차원량이다.
- 공조 및 냉각탑 해석에 사용되는 습공기의 비체적은 건공기 단위 무게당 습공기의 부피로 상태방정식 (pdaV = ndaRT) 으로부터 비체적 관계식을 유도할 수 있다.
- 아래 수식에 사용된 기호의 의미는
  - V : 습공기의 체적, ㎥
  - Mda : 건공기의 질량, kg [= 건공기 비분자량 (Relative Molecula of Dry Air) * 건공기 몰 수(Number of Moles of Dry Air]
  - nda : 건공기의 몰 수, mol (물질에 있는 입자의 수)
  - R : 일반기체상수 (Universal Gas Constant), 8314.41 J/(kmol∙K))
  - Rda : 건공기 기체상수 (Dry Air Gas Constant), 8314.41 / 28.9645 = 287.055 J/(kg∙K))
  - T : 절대온도, K
  - p : 대기압, N/㎡ (p = pda + pw)
  - pda : 건공기의 부분압, N/㎡
  - pw : 수증기의 부분압, N/㎡
  - W : 절대습도, kg vapor/kg dry air
- v = V / Mda = V / (건공기 비분자량 * 건공기 몰 수) = V / (28.9645 * nda)= (ndaRT / pda) / (28.9645 * nda) = RT / (28.9645 * (p – pw)) = RdaT / (p – pw)
- 아래의 “11. 건공기와 습공기의 기체상태식 관계”에서 유도한 식 ⑩ W = 0.62198 * (pw / (p – pw)을 (p – pw)에 대해서 풀면 (p – pw) = 0.62198 * pw / W를 얻을 수 있으며 또한 식 ⑩을 pw에 대해 풀면
  - W * (p – pw) = 0.62198 pw
  - W * p – W * pw = 0.62198 pw
  - W * p = (0.62198 + W) * pw
  - ∴ pw = W * p / (0.62198 + W)
- (p – pw) = 0.62198 * pw / W = 0.62198 W * p / (0.62198 + W) / W = 0.62198 p / (0.62198 + W)
  - 이 결과를 위 식 v = RT / (28.9645 * (p – pw))의 우변 (p – pw)에 대입하면,
- v = RT / (28.9645 * 0.62198 p / (0.62198 + W) = RT * (0.62198 + W) / (28.9645 * 0.62198 p) = RT * 0.62198 * (1 + 1 / 0.62198 * W ) / (28.9645 * 0.62198 p) = RT * ( 1 + 1.6078 W) / 28.9645 p
  - (참고: 위 식에서 0.62198은 수증기의 분자량 (18.01528 ㎏/kmol)에 건공기의 분자량 (28.9645 ㎏/kmol)의 비이며, 1.6078 은 건공기의 분자량에 수증기 분자량의 비이다.)
- 위 식의 R / 28.9645 = Rda = 8314.41 / 28.9645 = 287.055 1882 ≒ 287.055 J/(㎏∙K) 임으로 임의의 온도에서의 비체적 v = 287.055 * (t + 273.15) * (1+ 1.6078 * W) / p에 의해서 계산된다.
상태방정식 (Equation of State)
- 습건식 밀폐식 냉각탑 (Wet/Dry Closed Circuit Cooling Tower, 또는 Hybrid Closed Circuit Cooling Tower)을 건식으로 열량설계를 할 때 자주 인용되는 식 중의 하나가 상태방정식이다. 이것에 대한 의미를 정확히 이해를 하여야 공기특성을 쉽게 이해할 수 있기 때문에 자세하게 설명을 하고자 한다.
- 영국의 물리학자 Rovert Bolye은 모든 기체는 온도를 일정하게 유지할 때 그 비체적은 압력에 반비례하여 변화한다는 것을 알아냈다. 즉, pv = Constant (여기서 p: 기체의 압력 ㎏/㎡, v: 비체적 ㎥/㎏)으로 표시된다. 이것을 보일의 법칙이라고 한다.
- 프랑스의 물리학자 Jacques Alexandre Charles는 모든 기체는 압력이 일정할 때 0℃에서 100℃까지 가열하면 1℃ 마다 0℃일 때의 체적의 1/273 씩 (정도가 높은 측정을 한 결과 1/273.15임이 밝혀짐) 증가함을 발견하였다. 즉, v/T = Constant (여기서 v: 비체적 ㎥/㎏, T: 절대온도 K)으로 표시된다. 이것을 샤르의 법칙이라고 한다. 이 관계식에 대해 유도를 하면 다음과 같다.
- 일정 압력하에서의 비체적과 온도와의 관계식을 0℃에서의 기체의 비체적 v₀에 대해 초기온도 t₁℃에서의 비체적 v₁㎥/㎏로 하고 온도가 t₂℃가 되었을 때의 비체적을 v₂ ㎥/㎏라고 하면 다음과 같은 식이 성립된다.
  - v₁ = v₀ * (1 + 1/273.15 * t₁)
  - v₂ = v₀ * (1 + 1/273.15 * t₂)
  - 위 두 식의 좌우변을 서로 나누고 우변을 정리하면,
  - v₁ / v₂ = {v₀ * (1 + 1/273.15 * t₁)} / {v₀ * (1 + 1/273.15 * t₂)} = (273.15 + * t₁) / (273.15 + t₂) = T₁ / T
  - 위 식은 다시 v₁ / T₁ = v₂ / T₂로 쓸 수 있음으로 v / T = Constant 가 성립됨을 알 수 있다. 즉, 이 관계식으로부터 기체의 비체적 ㎥/㎏은 그 절대온도 TK에 비례한다.
- 보일의 법칙은 기체 압력 p와 비체적 v의 관계를 표시하며, 샤르의 법칙은 절대온도 T와 비체적 v간의 관계를 표시함으로 두 법칙을 하나로 정리하면 기체의 압력 p, 비체적 v, 절대온도 T의 관계가 구해진다. 즉, pv/T = Constant하게 된다. 이 정수를 R로 표기하면 pv/T = R 또는 pv = RT가 성립된다. 이 관계식을 일반적으로 상태방정식이라고 하며 또한 보일-샤르의 법칙이라고도 한다.
- 여기서 R을 가스정수 (Gas Constant)라고 하며, 기체의 종류에 따라 정해진다. 공기의 가스정수를 구해 본다. 표준상태 (0℃, 1 atm)에서의 공기의 압력 p = 10332.276 ㎏f/㎡, 공기의 비중량 γ = 1.29226026 ㎏/㎥, 절대온도 T = 273.15K임으로 이 값을 상태방정식에 대입하면,
  - Ra = p / (γT) = 10332.276 ㎏f/㎡ / (1.29226026 ㎏/㎥ * 273.15K) = 29.27148832 ㎏f∙m/㎏K ≒ 29.27 ㎏f∙m/㎏K= 29.27148832 * 9.80665 N∙m/㎏K = 287.0552409 J/㎏K ≒ 287.055 J/㎏K
  - 위 가스정수 Ra 는 공기 1㎏을 1K 높이는데 필요한 열량인 비열의 단위와 같다. 따라서 가스정수 R은 1㎏의 기체를 등압하에서 온도 1K 높이는데 필여한 외부의 일이라고 할 수 있다. 임의의 기체의 가스정수는 공기의 가스정수 Ra 를 근거로 하여 공기에 대한 그 기체의 비중 δ로부터 구할 수 있다.
  - 즉, R = Ra / δ
- “모든 기체의 1 kmol은 동일 온도 및 압력하에서는 동일한 체적을 갖는다”는 것을 Avogadro가 밝혔다. 이것을 아보가드로 법칙이라고 하며, 표준상태 (0℃, 1 atm) 하에서 그 체적은 22.4136 ㎥가 된다. 또 아보가드로의 법칙은 물질 1 kmol 중의 분자량은 모든 물질에 있어서 같다고 표현할 수도 있다. 물질 1 mol 중의 분자의 개수를 아보가드로수라고 하며 이 수는 6.02216 * 10^23이다.
- 기체의 분자량을 M이라고 하면 그 기체의 1 kmol의 중량은 M㎏이므로 표준상태하에서 완전가스의 특성식 (중량 G㎏의 기체에 대한 완전 가스의 상태식은 pv*G = pV = GRT ㎏∙m)은 pV = MRT가 된다.
  - 10332.276 ㎏f/㎡ * 22.4136 ㎥ = MR * 273.15
  - ∴ MR = 10332.276 * 22.4136 / 273.15 = 847.8254 ㎏f∙m/(kmol∙K) ≒ 847.8 ㎏f∙m/kmolK = 847.8254 * 9.80665 N∙m/(kmol∙K) = 8314.3 J/(kmol∙K)
    - (참고: SI단위에서 MR = 8314.41 J/(kmol∙K)로 고려하고 있다.)
  - R = 848 / M ㎏f∙m/㎏K 관계식이 성립되어 기체의 분자량 M을 알면 가스정수 R을 계산할 수 있다. 완전가스특성식은 pv = 848 / M∙T와 같이 다시 쓸 수 있다.
습도 (Humidity)
- 대기는 건공기 (Dry Air)와 수증기 (Water Vapor)의 혼합기체인 습공기 (Moist Air)로 각각은 완전기체의 상태식을 따르는 것으로 간주되며 Dalton의 법칙 (서로 다른 여러 종류의 완전기체를 한 용기내에서 혼합시킬 때 한 종류의 기체만이 용기 전체에 퍼진 경우와 동일한 압력을 갖으며 혼합기체의 전압력은 각각의 기체의 분압의 합과같다.)이 적용된다고 생각해도 무방하다.
- 습도는 습공기 중의 수증기의 비율이며 ASHRAE 기초 핸드북에 따르면 다음과 같이 여러 의미로 구분한다.
  - Humidity Ratio (절대습도, 일명 수분량비 (Moisture Content Ratio), 또는 혼합비 (Mixing Ratio)) W: 습공기 중 건공기 무게에 수증기의 무게의 비로 정의한다. 또한, 습도비는 분자량의 비 (물의 분자량 / 건공기의 분자량 = 18.01528 ㎏/mole / 28.9645 ㎏/mole = 0.62198)를 곱한 몰비 또는 몰분율비(Mole Fraction Ratio)와 동일하다.
    - (참고: 열역학에서 말하는 절대습도의 의미와 같다. 이 습도에 의하면 습공기의 온도가 변화하여도 절대습도 W는 일정함으로 냉각탑 및 공기조화에서 이용된다.)
- 아래 수식에 사용된 기호의 의미는 다음과 같다.
  - W : 절대습도, kg vapor/kg dry air
  - Mw : 수증기의 질량, kg
  - Mda : 건공기의 질량, kg [= 건공기 비분자량 (Relative Molecula of Dry Air) * 건공기 몰 수 (Number of Moles of Dry Air]
  - xw : 수증기의 몰 분량
  - xda : 건공기의 몰 분량
  - R : 일반기체상수 (Universal Gas Constant), 8314.41 J/(kg∙kmol∙K))
  - Rda : 건공기 기체상수 (Dry Air Gas Constant), 8314.41 / 28.9645 = 287.055 J/(kg∙K))
  - T : 절대온도, K
  - p: 대기압, N/㎡ (p = pda + pw)
  - pda: 건공기의 분압, N/㎡
  - pw: 수증기의 분압, N/㎡
- W = Mw / Mda —– ①
- W = 18.01528 xw / 28.9645 xda = 0.62198 xw / xda —– ②
  - (수증기의 몰 분량 xw는 수증기의 분압과 습공기의 전압비, 즉 xw = pw / p 이며, 건공기의 몰 분량 xda 는 건공기의 분압과 습공기의 전압비, 즉 xda = pda / p)
  - Specific Humidity (비습도) γ: 습공기의 무게에 수증기의 무게 비
- γ = Mw / (Mw + Mda ) —– ③
- 위 식 ①을 Mda에 대해 풀어서 식 ③에 대입하고 정리하면 비습도는
  - γ = Mw / (Mw + Mw / W) = 1 / (1 + 1/W) = W / (1 + W)
    - Absolute Humidity (일명 수증기 밀도 (Water Vapor Density) dv : 체적에 수증기의 무게 비
    - (참고: 이 습도의 영어 명칭을 우리 말로 번역하면 절대습도이나 일반적으로 열역학에서 다루는 의미와 다르며 위의 Humidity Ratio (습도비)가 우리가 흔히 말하는 절대습도에 해당함을 주지하기 바람.)
  - dv = Mw / V
- 습공기의 비체적 (Moist Air Specifiv Volume) v 는 건공기 단위 무게당 전체 체적으로 다음과 같이 표기된다.
- v = V / Mda (㎥/㎏da)—– ④
- 습공기의 밀도 (Density) ρ는 전체 체적에 전체 무게비임으로 다음과 같이 표기되며 식 ④을 전체체적 V에 대해 풀어 대입하면,
  - ρ = (Mw + Mda) / V = (Mw + Mda) / (v * Mda) = 1 / v * (Mw /Mda + 1) = 1 /v (W + 1)
    - Saturation Humidity Ratio (포화절대습도) Ws: 동일한 온도 t와 압력 p에서 물에 대해 포화된 습공기의 절대습도 (Humidity Ratio)
    - Degree of Saturation (포화도) μ: 동일한 온도와 압력에서 포화된 습공기의 습도비 Ws 에 공기 습도비 W의 비
- μ = W / Ws —– ⑤
  - Relative Humidity (상대습도) φ: 동일한 온도와 압력에서 포화된 습공기의 몰 분량 (xws)에 수증기의 몰 분량의 비 (xw) 또는 습공기의 온도에 대한 수증기의 포화압력 (pws)과 습공기 중의 수증기 분압 (pw)과 의 비. 따라서 습공기의 온도가 변화면 포화증기압 ps가 변화하기 때문에 수증기분압에 변화가 없어도 상대습도는 변화한다.
  - (참고: 포화증기압 (ps)은 포화습공기에서 물의 증기압으로 동일 조건의 순수한 물의 포화증기압 (pws)와 무시할 정도로 비슷하다. 따라서 동일한 압력과 온도에 순수한 물의 포화증기압 (pws) 대신에 사용될 수 있다.)
- φ = xw / xws = pw / pws —– ⑥
노점온도 (Dew Point Temperature) td
- 습공기를 일정한 압력하에서 온도를 내리면 수증기의 압력 (pw)은 일정하며 pw < pws 이지만 온도를 더욱 내리면 포화수증기압 (pws)가 저하하므로 상대습도가 증가한다. 그리고 온도를 내려 pw = pws 가 되는 온도를 노점온도라 한다. 즉, 상대습도 100%가 되는 온도가 노점이다. 이 온도보다 내려가면 수증기는 응축하여 안개나 이슬이 된다.
건공기와 습공기의 기체상태식 관계
- 건공기 (Dry Air)에 대한 상태식: pdaV = ndaRT
- 수증기 (Water Vapor)에 대한 상태식: pwV = nwRT
- 습공기 (Moist Air)에 대한 상태식: (pda + pw) V = (nda + nw)RT
- 아래 수식에 사용된 기호의 의미는 다음과 같다.
  - xw: 수증기의 몰 분량
  - xda: 건공기의 몰 분량
  - pda: 건공기의 부분압, N/㎡
  - pw: 수증기의 부분압, N/㎡
  - pws: 수증기 포화압, N/㎡
  - φ: 상대습도
  - W: 절대습도 (Humidity Ratio)
  - Ws: 포화 비습도 (Humidity Ratio @ Saturation) 절대습도는 0에서 포화 비습도까지 값을 갖는다
- xda = pda / p = pda / (pda + pw) —– ⑦
- xw = pw / p = pw / (pda + pw) —– ⑧
- xda + xw = 1 —– ⑨
- 위 식 과 ⑧를 위 식 ②에 대입하면 습도비 (일명 절대습도)는
  - W = 0.62198 * pw / pda = 0.62198 * pw / (p – pw) —– ⑩
  - Ws = 0.62198 * pws / (p – pws) —– ⑪
  - 위 식에서 pws는 주어진 온도에서 건공기가 없는 상태의 수증기의 포화압력 (Saturation Pressure)을 나타낸다. 이 압력은 온도만의 함수이며 포화된 습공기에서 물의 증기압 (Vapor Pressure)과는 약간 다르다.
- 위 식 ⑩을 pda에 대해 풀면 pda = 0.62198 pw / W을 얻고 이 결과를 위 식 ⑦에 대입하면
  - xda = (0.62198 pw / W) / (0.62198 pw / W + pw) = (0.62198 / W) / (0.62198 / W + 1) = (0.62198 / W) / {(0.62198 + W)/ W} = 0.62198 / (0.62198 + W) = 1 / (1 + 1 / 0.62198 * W) = 1 / (1 + 1.6078 W)
- 즉, xda = 1 / (1 + 1.6078W) 관계식이 성립하며 절대습도 값이 주어지면 무차원 수인 건공기의 몰분량 (Mole Fraction) 값을 구할 수 있다. 이 값을 이용하여 건공기의 분압은 위 식 ⑦로부터 계산해 낼 수 있다. 즉, pda = xda * p
- 위 식 ⑩을 pda에 대해 풀면 pda = 0.62198 pw / W을 얻고 이 결과를 위 식 ⑧에 대입하면
  - xw = pw / (0.62198 pw / W + pw) = 1 / (0.62198 / W + 1) = 1 / {(0.62198 + W)/ W} = W / (0.62198 + W)
- 즉, xw = W / (0.62198 + W) 관계식이 성립하며 절대습도 값이 주어지면 무차원 수인 수증기의 몰분량 (Mole Fraction) 값을 구할 수 있다. 이 값을 이용하여 건공기의 분압은 위 식 ⑧로부터 계산해 낼 수 있다. 즉, pw = xw * p
- 포화수증기 xws = 상대습도 * xw 임으로 상대습도 값과 절대습도 값을 알면 구할 수 있다.
  - 가령 대기압이 101325 N/㎡, 건구온도가 30℃, 절대습도가 0.0215 ㎏ vapor/㎏ dry air인 습공기에 대해 건공기 및 수증기의 몰 분량과 각각의 분압을 구해 보면,
    - xda = 1 / (1 + 1/ 0.62198 * W) = 1 / (1 + 1 / 0.62198 * 0.0215) = 0.966588
    - pda = xda * p = 0.966588 * 101325 = 97939.52 N/㎡
    - xw = W / (W + 0.62198) = 0.0215 / (0.0215 + 0.62198) = 0.033412
    - xw = 1 – xda = 1 – 0.966588 = 0.033412
    - pw = xw * p = 0.033412 * 101325 = 3385.48 N/㎡
    - pw = p – pda = 101325 – 97939.52 = 3385.48 N/㎡
  - 건구온도 30℃에서의 수증기 포화압 (Water Vapor Saturation Pressure) pws는 증기압표 또는 Hyland-Wexler 식 또는 Goff 식을 이용하여 계산한다.
    - pws by Hyland-Wexler’s Equation = 4246.0302 N/㎡
      - Ws = 0.62198 * pws / (p – pws) = 0.62198 * 4246.0302 / (101325 – 4246.0302) = 0.027204
      - φ = pw / pws = 3385.49 / 4246.0302 = 0.79733 = 79.733%
      - xws = xw / φ = 0.033412 / 0.79733 = 0.04190
      - μ = W / Ws = 0.0215 / 0.027204 = 0.79032
    - pws by Goff’s Equation = 4242.5947 N/㎡
      - Ws = 0.62198 * pws / (p – pws) = 0.62198 * 4242.5947 / (101325 – 4242.5947) = 0.027181
      - φ = pw / pws = 3385.48 / 4242.5947 = 0.79797 = 79.797%
      - xws = xw / φ = 0.033412 / 0.79797 = 0.04187
      - μ = W / Ws = 0.0215 / 0.027181 = 0.79099
    - 위 두 결과를 비교하면 매우 근사함을 알 수 있다. 상대습도 값에 있어 좀더 엄격한 것이 백연 설계에 유리함으로 Kroger 교수가 추천한 Goff 식을 모든 프로그램에 적용함을 밝혀둔다.
- 다음은 위에서 기술한 식 ②, ⑤ 및 ⑥을 이용하여 상대습도 φ 및 포화절대습도 (Saturation Humidity Ratio)와 포화도와의 관계식을 유도해 본다.
  - 식 ⑨ xda + xw = 1 는 xda = 1 – xw로 변환하여 ②의 분모항에 대입하면,
    - W = 0.62198 * xw / xda = 0.62198 * xw / (1 – xw) = μWs —– ⑫
  - 식 ⑫로부터 포화절대습도 관계식을 다음과 같이 유추할 수 있다.
    - Ws = 0.62198 * xws / (1 – xws) —– ⑬
  - 식 ⑫을 xw에 대해 풀어서 정리하면,
    - μWs (1 – xw) = μWs – μWs xw = 0.62198 xw
    - xw (0.62198 + μWs ) = μWs
    - xw = μWs / (0.62198 + μWs)
  - 식 ⑬을 xws에 대해 풀어서 정리하면,
    - Ws (1 – xws) = Ws – Ws xws = 0.62198 xws
    - xws (0.62198 + Ws) = Ws
    - xws = Ws / (0.62198 + Ws)
  - 위의 결과값을 식 ⑥ φ = xw / xws 에 대입하고 포화도에 대해 정리하면,
    - φ = xw / xws = {μWs / (0.62198 + μWs)} / {Ws / (0.62198 + Ws)}
    - φ Ws / (0.62198 + Ws) = μWs / (0.62198 + μWs)
    - φ Ws (0.62198 + μWs) = μWs (0.62198 + Ws)
    - 0.62198 φ + φ μWs = 0.62198 μ + μWs
    - 0.62198 φ = 0.62198 μ + μWs – φ μWs = μ {0.62198 + (1 – φ ) Ws}
  - μ = 0.62198 φ / {0.62198 + (1 – φ ) Ws} = φ / {1 + (1 – φ ) Ws / 0.62189} —– ⑭
- 위 식 ⑭는 상대습도와 포화절대습도 값을 이용하여 포화도를 계산하는 식을 나타낸 것이다. 포화도 값을 알면 습구온도와 건구온도 값을 이용하여 절대습도를 계산하여 상대습도를 계산할 때 이용된다.
  - φ = (0.62198 μ + μWs) / (0.62198 + μWs) = (0.62198 μ + W) / (0.62198 + W)
- 또한 위 식 ⑪ Ws = 0.62198 pws / (p – pws)을 이용하여 위 식의 우변항의 Ws에 대입하고 정리하면,
  - φ = μ (0.62198 + Ws) / (0.62198 + μWs) = μ / {(0.62198 + μWs) / (0.62198 + Ws)}
  - = μ / [{(0.62198 + 0.62198 μ pws / (p – pws))} / {(0.62198 + 0.62198 pws / (p – pws))}]
  - = μ / [{(1 + μ pws / (p – pws))} / {(1 + pws / (p – pws))}]
  - = μ / [{(p – pws + μ pws) / (p – pws)} / {(p – pws + pws) / (p – pws)}]
  - = μ / {1 – (1 – μ) pws/ p}
- 다음은 위 식 ⑥ φ = pw / pws를 pw에 대해 풀어서 식 ⑩의 우변항에 대입하여 상대습도 φ에 대해 정리하면 절대습도와 상대습도 간의 관계식을 구할 수 있다.
  - W = 0.62198 * pw / (p – pw) = 0.62198 * φ pws / (p – φ pws)
  - W (p – φ pws) = 0.62198 * φ pws
  - W p – φ pws W = 0.62198 * φ pws
  - W p = φ (0.62198 * pws + pws W) = φ pws (0.62198 + W)
- ∴ φ = W p / {pws (0.62198 + W)}
비 엔탈피 (Specific Enthalpy)
- 어느 상태에서의 건공기 단위 질량 당 습공기가 갖는 전 열량을 비 엔탈피라하며 간단히 엔탈피 라고 호칭한다. 습공기의 엔탈피는 건공기의 엔탈피 및 수증기의 엔탈피의 합이다. 0℃ 건공기의 엔탈피는 0 이며, 0℃ 물의 엔탈피 역시 0 이다. 습공기의 엔탈피 h는 다음 관계식이 성립된다.
- h = hda + Whg
  - hda: 건공기의 비 엔탈피 (kJ/㎏)
  - hg: 습공기의 온도에서 포화되는 수증기의 비 엔탈피 (kJ/㎏)
  - W: Humidity Ratio (㎏ water vapor / ㎏ dry air)
- ASHREA 기초 핸드북에 의거하면 건공기 및 수증기의 비 엔탈피는 다음과 같다.
  - hda ≒ 1.006 t
  - hg ≒ 2501 + 1.805 t
  - ∴ h = 1.006 t + W(2501 + 1.805t)
- Kroger가 제안한 습공기의 비 엔탈피는 다음과 같다.
  - 습공기 비 엔탈피 = 건공기 정압비열 * 습공기의 섭씨온도 + 습공기의 절대습도 * (증발잠열 + 수증기의 정압비열 * 습공기의 절대온도)
    - 참고: 위 식에서 건공기 및 수증기 정압비열은 절대온도 / 2에서의 값을 사용하며, 증발잠열은 0℃에서의 값인 2.5016 x 10^6 J/㎏을 사용하여야 한다.
    - 참고: 비 엔탈피를 절대온도 K로 나눈 값이 엔트로피 (Entropy)이며 정의는 단위 질량 당 가열량을 그 때의 절대온도로 나눈 것이다. 엔트로피는 열량설계에서는 사용하지 않는다.
절대습도 계산 관계식 유도
- 앞서 다룬 모든 식은 절대습도 값이 주어져야 계산이 됨으로 절대습도 값을 계산하는 식이 필요하다. 절대습도 값을 계산하는 관계식의 유도는 다음과 같다.
- 절대습도 식을 유도하기 위해서는 먼저 열역학적 습구온도에 대한 비 엔탈피를 계산하는 식을 세워야 한다. 열역학적 습구온도란 습공기의 어떤 상태에 대해 정확하게 동일한 온도와 전압 (Total Pressure)에서 액상의 물이 공기로 증발되어 포화상태에 도달하는 온도가 존재하는데 이 온도를 가르켜 열역학적 습구온도라 한다. 이 온도에서의 비 엔탈피 hs는 다음과 같은 식으로 계산된다.
- 동일한 압력하에서 단열 포화과정애서 다음의 3가지 이론이 성립된다.
  - 절대습도 (Humidity Ratio)는 주어진 초기 절대습도 W으로부터 습구온도 twb에서 포화되는 포화 절대습도 (Saturation Humidity Ratio) Ws로 증가된다.
  - 비 엔탈피는 주어진 초기 값 h로부터 습구온도 tbw에서 포화되는 비 엔탈피 hs로 증가된다.
  - 건공기 단위 질량 당 추가되는 물의 질량은 (Ws – W)임으로 습공기에 에너지를 추가되는 에너지의 량은 (Ws – W)hw 가 된다. 여기서 hw는 습구온도 twb에서 추가되는 물의 비 엔탈피이다. hw ≒ 4.186047 twb이다. (여기서 twb는 ℃임.)
- 위 이론을 수식으로 표현하면 hs = h + (Ws – W)hw가 되며 이 식을 절대습도 W에 대해 풀어서 정리하면 다음과 같다.
- 습공기에 대한 비 엔탈피 계산식을 포화공기에 대해 적용할 수 있음으로 twb에서의 비 엔탈피 hs는 다음과 같다.
  - hs = 1.006 twb + Ws(2501 + 1.805 twb)
  - hs = h + (Ws – W)hw = h + Wshw – Whw = 1.006 tdb + W(2501 + 1.805 tdb) + Wshw – Whw
  - W = (hs – Wshw – 1.006 tdb) / {(2501 + 1.805 tdb – hw)}
  - = {1.006 twb + Ws(2501 + 1.805 twb) – 4.186047 twb Ws – 1.006 tdb)} / {(2501 + 1.805 tdb – 4.186047 twb)}
  - = {(2501 -2.381047 twb) Ws – 1.006 (tdb – twb)} / {(2501 + 1.805 tdb – 4.186047 twb)}
  - (참고: 절대습도를 계산하는 위 식에서 포화 절대습도 Ws는 반듯이 습구온도에서의 값을 사용하여야 함을 주지하기 바람.)
- Dr. Kroger는 ASHREA 핸드북에 기술한 절대습도 관계식에 보정치와 포화증기압에 1.005의 보정치를 적용한 포화절대습도 값을 사용하여 다음과 같이 제시하였다. 열량설계에서는 Dr. Kroger가 제시한 관계식을 사용함을 참고 바람.
  - W = {(2501.6 -2.3263 twb) Ws – 1.00416 (t db – twb)} / {(2501.6 + 1.8577 tdb – 4.184 twb)}
  - Ws = 0.62198 * 1.005 * pws / (p – 1.005 * pws) = 0.62509 * pws / (p – 1.005 * pws)